计算机组成与体系结构
数据的表示
R进制转十进制使用按权展开法
其具体操作方式为:将 R 进制数的每一位数值用 Rk 形式表示,即幂的底数是 R,指数为 k ,k 与该位和小数点之间的距离有关。当该位位于小数点左边,k 值是该位和小数点之间数码的个数,而当该位位于小数点右边,k 值是负值,其绝对值是该位和小数点之间数码的个数加 1 。
例如:二进制 10100.01 =1 x 24 + 1 x 22 + 1 x 2-2
例如:七进制 604.01= 6 x 72 + 4 x 70 + 1 x 7-2
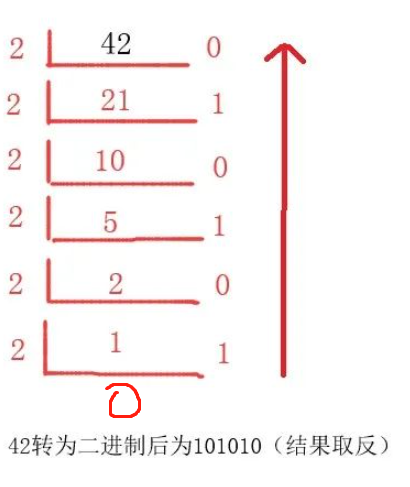
十进制转R进制使用短除法
将 42 转换为二进制数。
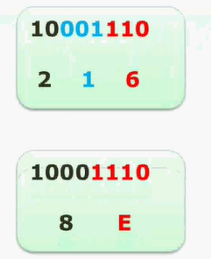
二进制转八进制与十六进制数
原码
原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值。例如 8 位二进制::
1 | [+1]原 = 0000 0001 |
反码
反码的表示方法是:
- 正数的反码是其本身。
- 负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
1 | [+1] = [00000001]原 = [00000001]反 |
补码
补码的表示方法是:
- 正数的补码就是其本身。
- 负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后 + 1。 (即在反码的基础上 + 1)
1 | [+1] = [00000001]原 = [00000001]反 = [00000001]补 |
原码、反码、补码的数值表示范围
| 数据类型 | 整数 |
|---|---|
| 原码 | -(2n-1-1)~2n-1-1 |
| 反码 | -(2n-1-1)~2n-1-1 |
| 补码 | -2n-1~2n-1-1 |
浮点数运算
浮点数表示:$N = M * R^e$
其中M称为尾数,e是指数,R为基数。
例题:两浮点数 x = 0.1101 201,y = (-0.1010)\211,求 x + y
对阶
求补码
[x]补 = 00,01;00.1101
[y]补 = 00,11;11.0110
求阶差
小阶向大阶对阶,同时尾数右移,移动位数为阶差。
00.11 - 00.01 = 00.10 = 2
阶差为 2
[x]补 = 00,11;00.0011
尾数求和
将对阶后的两个尾数按定点加减运算规则进行运算。
上述对阶后得:[x]补 = 00,11;00.0011 [y]补 = 00,11;11.0110
[x+y]补=00,11;11.1001。规格化
左规
尾数出现 00.0xx…x 或 11.1xx…x 时需要进行左规,左规时尾数左移一位,阶码减一,直到成为:00.1xx…x 或 11.0xx…x。即尾数第一位和符号位相同。
如上例求和结果为:
[x+y]补= 00,11;11.1001
故将其尾数左移一位,阶码减一,得:
00,10;11.0010
规格化后这是补码,求其尾数的原码即可,故结果为
x + y = (-0.1110) * 210右规
当尾数出现01.xx…x或10.xx…x时表示尾数溢出,需要进行右归,右归时尾数右移,阶码加1。即两位符号位的数值不相同(01 / 10)。
例题:已知浮点数 x = 0.1101 x 210,y = 0.1011 x 201,求 x + y对阶:
求补码:$[x]补 = 00,10;00.1101,[y]补 = 00,01;00.1011$
求阶差:$00,10 - 00,01 = 00,01 = 1 ,故阶差为 1 ,故[y]_补=00,10;00.0101$
尾数求和:
$[x+y]_补 = 00,10;01.0010$
故需要进行右规,尾数向右移动一位,阶码加 1 得:
$$
[x+y]补 = 00,11;00.1001 \
x + y = 0.1001 * 2^{11}
$$
舍入
舍入,是指数据的长度超过了计算机当中存储数据的物理器件所保存的数据长度。低位部分就要进行处理,保证数据能够以比较精确的精度保存在计算机当中。
在对阶和右规过程中,可能出现尾数末位丢失,引起误差。为了尽可能减小误差,就需要考虑舍入。
舍入的方法:
截断法
将移出的数据一律舍去。该方法简单,很常用。但是影响精度。
0舍1入法
移掉的是1,则尾数末尾加 1,移掉的是 0,就不加。
恒置“1”法
将要保留的末位数据恒置 1,无论右移掉的是 1 还是 0,末位是 1 还是 0。
计算机结构
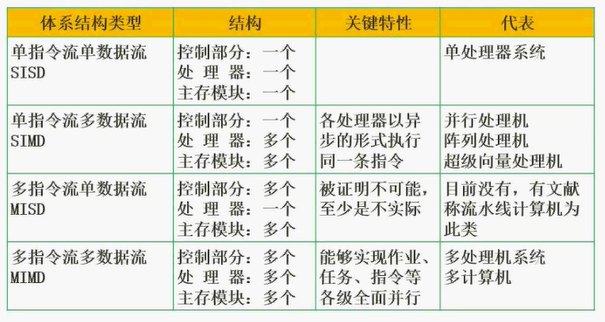
计算机体系结构分类 - Flynn
流水线
流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。各种部件同时处理是针对不同指令而言的,它们可同时为多条指令的不同部分进行工作,以提高各部件的利用率和指令的平均执行速度。
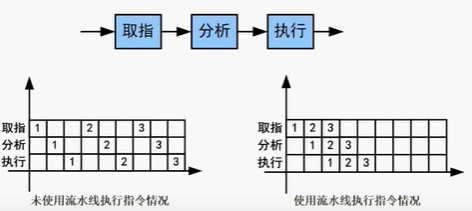
流水线计算
流水线周期为执行时间最长的一段
流水线计算公式为:1 条指令执行时间 + (指令条数 - 1) 流水线周期
理论公式(At 为流水线周期):$(t1+t2+..+ tk)+(n-1)At$
实践公式(At 为流水线周期,k 为几部分):$kAt+(n-1)At$
例题:若指令流水线把一条指令分为取指、分析和执行三部分,且三部分的时间分别取指 2ns,分析 2ns,执行 1ns。那么,流水线周期是多少?100条指令全部执行完毕需要的时间是多少?
流水线周期:2ns
理论公式:$(2+2+1)+(100-1)* 2 = 203$
实践公式:$32+(100-1)2 = 204$
流水线吞吐率计算
流水线的吞吐率(Though Put rate,TP)是指在单位时间内流水线所完成的任务数量或输出的结果数量。计算流水线吞吐率的最基本的公式如下:
$$
TP =\frac{指令条数}{流水线执行时间}
$$
流水线最大吞吐率:
$$
TP_{max}=\lim_{n\rightarrow+\infty}\frac{n}{(k+n-1)\Delta{t}}=\frac{1}{\Delta{t}}(\Delta{t}为流水线周期)
$$
例题:若指令流水线把一条指令分为取指、分析和执行三部分,且三部分的时间分别取指 2ns,分析 2ns,执行 1ns。请计算吞吐率和最大吞吐率。
吞吐率:$TP=\frac{100}{203}=0.49$
最大吞吐率:$TP_{max}=\frac{1}{2}=0.5$
流水线的加速比
完成同样一批任务,不使用流水线所用的时间与使用流水线所用的时间之比称为流水线的加速比。计算流水线加速比的基本公式如下:
$$
S=\frac{不使用流水线的执行时间}{使用流水线的执行时间}
$$
例题:若指令流水线把一条指令分为取指、分析和执行三部分,且三部分的时间分别取指2ns ,分析2ns,执行1ns。请计算流水线的加速比。
$$
S=\frac{(2+2+1)100}{(2+2+1)+(100-1)2}=\frac{500}{203}=2.46
$$
流水线的效率
流水线的效率是指流水线的设备利用率。在时空图上,流水线的效率定义为 n 个任务占用的时空区与k个流水段总的时空区之比。
计算流水线效率的公式:
$$
E=\frac{n个任务占用的时空区}{k个流水段总的时空区}=\frac{T_0}{KT_k}
$$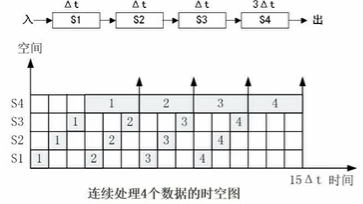
$$
E=\frac{(\Delta{t}+\Delta{t}+\Delta{t}+3\Delta{t})4}{415\Delta{t}}=0.4
$$
层次化存储结构
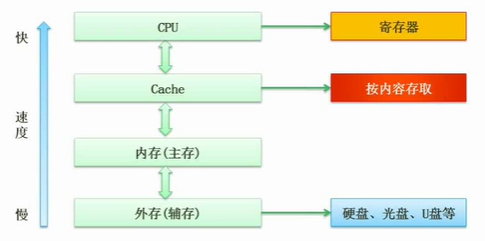
Cache
Cache 的功能:提高 CPU 数据输入输出的速率,突破冯●诺依曼瓶颈,即 CPU 与存储系统间数据传送带宽限制。
在计算机的存储系统体系中,Cache 是访问速度最快的层次。
使用 Cache 改善系统性能的依据是程序的局部性原理。
如果以 h 代表对 Cache 的访问命中率,t1 表示 Cache 的周期时间,t2 表示主存储器周期时间,以读操作为例,使用 Cache + 主存储器 的系统的平均周期为 t3,则:
$t_3 = ht_1+(1-h)t_2$
其中,(1 - h) 又称为失效率(未命中率)。
例题:Cache的访问命中率为95%,Cache的周期时间为1ns,主存储器周期时间为1ms(1ms=1000ns),以读操作为例,求使用 Cache + 主存储器 的系统的平均周期。
$t_3 = ht_1+(1-h)t_2=95\%1ns+(1-95\%)1000ns=50.95ns$
局部性原理
- 时间局部性
- 空间局部性
工作集理论:工作集是进程运行时被频繁访问的页面集合。
主存储器
主存储器编址
例题:内存地址从 AC000H 到 C7FFFH,共有多少 K 个地址单元?如果该内存地址按字(16bit)编址,由 28 片存储器芯片构成。已知构成此内存的芯片每片有 16K 个存储单元,则该芯片每个存储单元存储多少位?
地址单元的个数:将内存大地址减去小地址再加 1
$C7FFFH-AC000H+1=1C000H(给7加的是16,因为是16进制)$
转为 K 个地址单元:将十六进制转成十进制再除以 1024
$\frac{16^4+12*16^3}{1024}=112K$
故共有 112K 个地址单元
设每个存储单元存储X位
$\frac{112K16}{2816K*X}=1$
得 X = 4
则每个存储单元存储 4 位
磁盘结构与参数
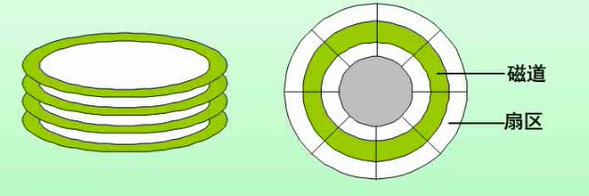
存取时间 = 寻道时间 + 等待时间(平均定位时间 + 转动延迟)
注意:寻道时间是指磁头移动到磁道所需的时间,等待时间为等待读写的扇区转到磁头下方所用的时间。
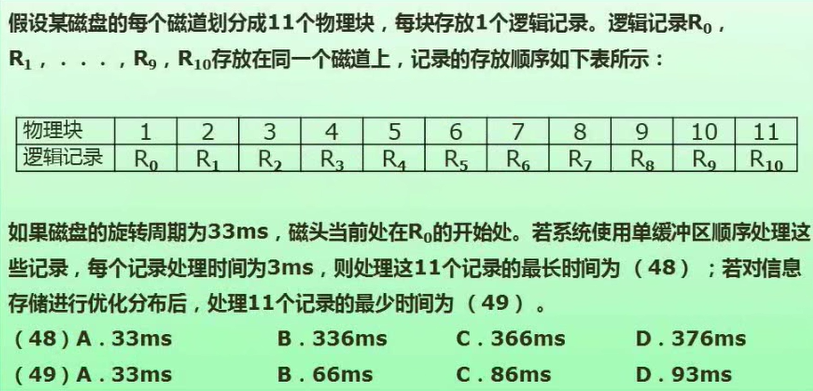
最长时间:
磁盘旋转周期为33ms,因此磁盘旋转一周时间为33ms,磁盘总共有11个物理块,所以每个物理块需要的读取时间为3ms。
磁头当前在R0开始处,所以数据从R0开始读取。
使用单缓冲区顺序处理记录,所以需要一条数据读取完毕并且处理完毕后才能读取下一条数据。
磁头首先读取出R0放在缓冲区处理。3ms之后R0读取完毕放入缓冲区,此时磁头位于R1的开始处,但是由于单缓冲区所以此时无法直接读取R1并对R1进行操作,于是磁盘继续转动,3ms之后R0处理完毕,此时磁头位于R2的开始处,并非我们需要处理的R1,因此磁盘继续转动寻找R1,直到再转一圈(33ms)到达R1的开始处开始读取R1(3ms)。
因此R0需要的时间为读取3ms加处理3ms,剩余R1到R10需要的时间为(33+3)*10=360ms,所以总处理时间为360+6=366ms。
最短时间:
在对数据进行重新排列后此时磁盘上数据的存储顺序为:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|
| R0 | R6 | R1 | R7 | R2 | R8 | R3 | R9 | R4 | R10 | R5 |
此时开始处理,磁头从R0开始处读取,读取(3ms)完毕后放入缓冲区处理(3ms),此时磁盘继续转动,R0处理完毕时此时磁头正好处于R1的开始处,开始对R1读取并处理。因此这是对存储优化分布之后最理想的读取情况,所需时间为:
(读取(3ms)+处理(3ms))*11=66ms。
总线
根据总线所处的位置不同,总线通常被分成三种类型,分别是:
- 内部总线
- 系统总线
- 数据总线
- 地址总线
- 控制总线
- 外部总线
系统可靠性分析
- 串联系统(所有都正常,系统才能正常运行)

$$
可靠度:R=R_1R_2…*R_n
$$
$$
失效率:\lambda=\lambda_1+\lambda_2+…+\lambda_n
$$
- 并联系统(一个正常,系统就正常)
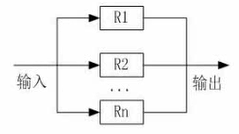
$$
可靠度:R=1-(1-R_1)(1-R_2)…*(1-R_n)
$$
$$
失效率:\mu=1-R
$$
- 模冗余系统(少见)
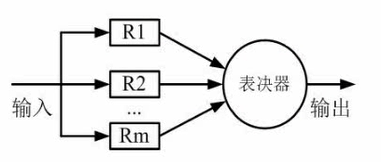
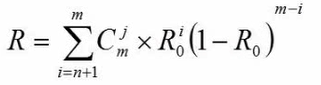
m是子系统的个数
- 混合系统(先看整体)
例题:
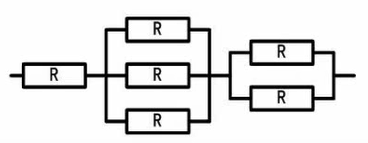
整体为串联系统,局部为并联系统
$$
R_1=R(1-(1-R)^3)(1-(1-R)^2)
$$
差错控制
什么是检错和纠错?
检测:检测错误。
纠错:检测出错误并纠正错误。
什么是码距?
一个编码系统的码距是整个编码系统中任意(所有)两个码字的最小距离。
例:
若用 1 位长度的二进制编码。若 A= 1, B = 0。这样A, B之间的最小码距为 1。
若用 2 位长度的二进制编码,若以 A = 11, B = 00为例,A、B之间的最小码距为 2。
若用 3 位长度的二进制编码,可选用 A = 111,B = 000作为合法编码。A, B之间的最小码距为 3。
码距与检错、纠错有何关系?
- 在一个码组内为了检测 x 个误码,要求最小码距 d 应该满足:d >= x + 1
- 在一个码组内为了纠正 x 个误码,要求最小码距 d 应该满足:d >= 2x + 1
CRC
什么是模2除法,它和普通的除法有何区别?
模 2 除法是指在做除法运算的过程中不计其进位的除法。
例题:10111对110进行模2除法为
普通除法运算过程:

模2除法运算过程:

例题:原始报文为11001010101,其生成多项式为:x4+x3+x+1。对其进行CRC编码后的结果为?
被除数:原始报文 + 生成多项式的最高次方个 0 = 110010101010000
除数:生成多项式有幂次就为 1,没有幂次就为 0 = 11011
被除数对除数进行模 2 除法运算

CRC编码:原始报文 + 余数 = 110010101010011
CRC编码对除数进行模2除法运算得出的余数为0,即传输的信息没有出错。
海明校验码
例题:求信息1011的海明码。
因信息1011有4位,故x=4,代入公式2r>=x+r+1,得2r>=4+r+1
故确定校验码为3位:23>=4+3+1。
分别放在20=1、21=2、 22=4 位。(分别放在20到2检验码的位数-1)
列出校验位公式。
$$
7=2^2+2^1+2^0
$$$$
6=2^2+2^1
$$$$
5=2^2+2^0
$$$$
3=2^1+2^0
$$$$
r_2 = I_4 \bigoplus I_3 \bigoplus I_2 \
r_1 = I_4 \bigoplus I_3 \bigoplus I_1 \
r_0 = I_4 \bigoplus I_2 \bigoplus I_1
$$| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
| :———–: | :———–: | :———–: | :———–: | :———–: | :———–: | :———–: | :—-: |
| I4 | I3 | I2 | | I1 | | | 信息位 |
| | | | r2 | | r1 | r0 | 校验位 |根据公式得r2=0,r1=0,r0=1。
$$
r_2 = I_4 \bigoplus I_3 \bigoplus I_2 = 1 \bigoplus 0 \bigoplus 1 = 0\
r_1 = I_4 \bigoplus I_3 \bigoplus I_1 = 1 \bigoplus 0 \bigoplus 1 = 0\
r_0 = I_4 \bigoplus I_2 \bigoplus I_1 = 1 \bigoplus 1 \bigoplus 1 = 1
$$将数据加入表格,如表所示。
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 信息位 | |||
| 0 | 0 | 1 | 校验位 |
海明码纠错:将收到的校验码异或正确的校验码转成十进制就知道哪个位置出错了。